Based on the principle of destructive interference of propagating acoustic waves, active noise control has wide applications in the cancelation of low frequency noise. However, when dealing with impulsive noise, the classic active noise control algorithm, such as filtered-x least mean square (FxLMS), converges slowly or even diverges.

Many practical acoustical signals are impulsive-like, such as noise generated by stamping machines in industrial manufacturing plants, or by life-saving equipments in hospitals, which can be more accurately modeled by alpha stable distribution than Gaussian one. Due to the inexistence of the second order statistics of alpha stable distribution, these traditional methods based on Gaussian assumptions like FxLMS, fail in these applications.

To provide such kind of robustness for the active impulsive noise control, robust active noise control algorithms have been developed. However, these methods either need a priori knowledge of alpha parameter or are sensitive to threshold parameters. Moreover, with the increase of heaviness of impulsive noise, all of these methods degrade severely, especially when α<1, where α is the stable parameter.

To suppress impulsive noise efficiently and effectively under various situations, researchers from the Key Laboratory of Noise and Vibration Research, Institute of Acoustics of the Chinese Academy of Sciences proposed a new filtered-x affine projection sign algorithm (NFxAPSA) for the active control of impulsive noise. The superior performance of the proposed algorithm in active control of impulsive noise with both synthesized and real-world data has been verified.

As derived by minimizing ℓ₁ norm of the posteriori error vector, NFxAPSA can provide robustness under impulsive noise contaminations. Furthermore, under the small step-size assumptions of regular active noise control algorithms, NFxAPSA has similar efficient implementation. The efficiency is due to the accurate approximation and recursive computation of a priori error vector.

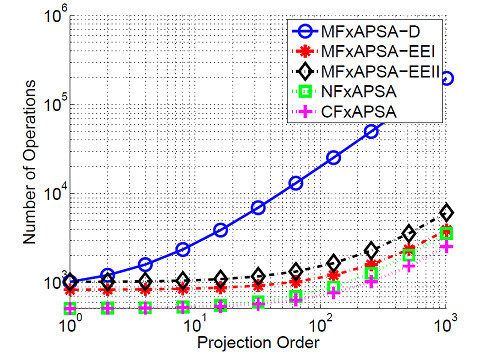
Fig. 1: The number of multiplications versus projection order for different implementations of APSA for active impulsive noise control. (Image by XIAO Longshuai). 

Similar as the conventional FxAPSA (CFxAPSA), the approximation takes much smaller operations than the exact one, i.e., modified filtered-x structure of APSA (MFxAPSA), which has been shown to cancel impulsive noise sources effectively. This result can be shown in Fig. 1, where the low complexity of NFxAPSA is shown.

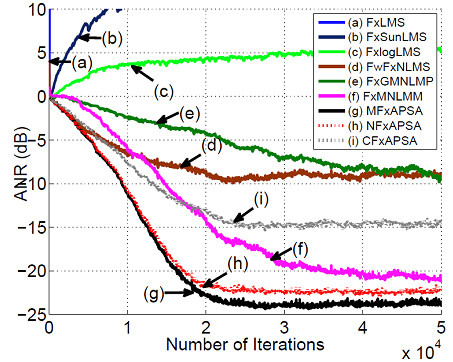
Fig. 2: The convergence curves of different active impulsive noise control algorithms for alpha stable impulsive noise, where the alpha parameter value is 0.6. (Image by XIAO Longshuai).

One typical active impulsive noise control performance validation result of NFxAPSA can be seen in Fig. 2. In this figure, NFxAPSA has similar convergence curve as the exact implementation ( MFxAPSA), while NFxAPSA has an outstanding performance over others.

Two variants of NFxAPSA, e.g., variable step-size and hybrid update strategies, also show the effectiveness of the proposed approximation method. Together with these extensions, more numerical results with both synthetic and real data show superior performance of the proposed algorithm.

Theory aspect to understand the statistical behavior of NFxAPSA and applicability of the new structure to other kind of affine projection algorithms when adapted to active noise control applications are two interesting issues for future research.

Reference: 

XIAO Longshuai, WU Ming and YANG Jun. A New Efficient Filtered-x Affine Projection Sign Algorithm for Active Control of Impulsive Noise. Signal Processing. DOI: 10.1016/j.sigpro.2015.09.015